Controlador de atitude

Nesta secção você irá implementar o controlador de atitude, que comanda os torques \(\tau_x\), \(\tau_y\) e \(\tau_z\) a partir da diferença entre os ângulos de Euler de referência \(\phi_r\), \(\theta_r\) e \(\psi_r\) e estimados \(\phi\), \(\theta\) e \(\psi\).

Para isto, será implementada uma nova função:

• attitudeController()

Além de uma alteração em uma função já previamente implementada:

• reference()

---

Implementação

Para começar, copie e cole o arquivo attitude_estimator.c e renomeie ele para attitude_controller.c.

Definições

Variáveis globais

Declare mais algumas variáveis globais, que são as referências dos ângulos de Euler que entram na função do controlador de atitude.

// System references
float phi_r, theta_r, psi_r; // Euler angles reference [rad]

Loop principal

Inclua no seu loop principal a chamada da função attitudeController() entre as funções attitudeEstimator() e mixer().

// Main application task
void appMain(void *param)
{
    // Infinite loop (runs at 200Hz)
    while (true)
    {
        reference();                  // Read reference setpoints (from Crazyflie Client)
        sensors();                    // Read raw sensor measurements
        attitudeEstimator();          // Estimate orientation (roll/pitch/yaw) from IMU sensor
        attitudeController();         // Compute desired roll/pitch/yaw torques
        mixer();                      // Convert desired force/torques into motor PWM
        actuators();                  // Send commands to motors
        vTaskDelay(pdMS_TO_TICKS(5)); // Loop delay (5 ms)
    }
}

Funções

Referência

Os ângulos de Euler de referência \(\phi_r\) e \(\theta_r\) serão comandados pelo Command Based Flight Control do Crazyflie Client.

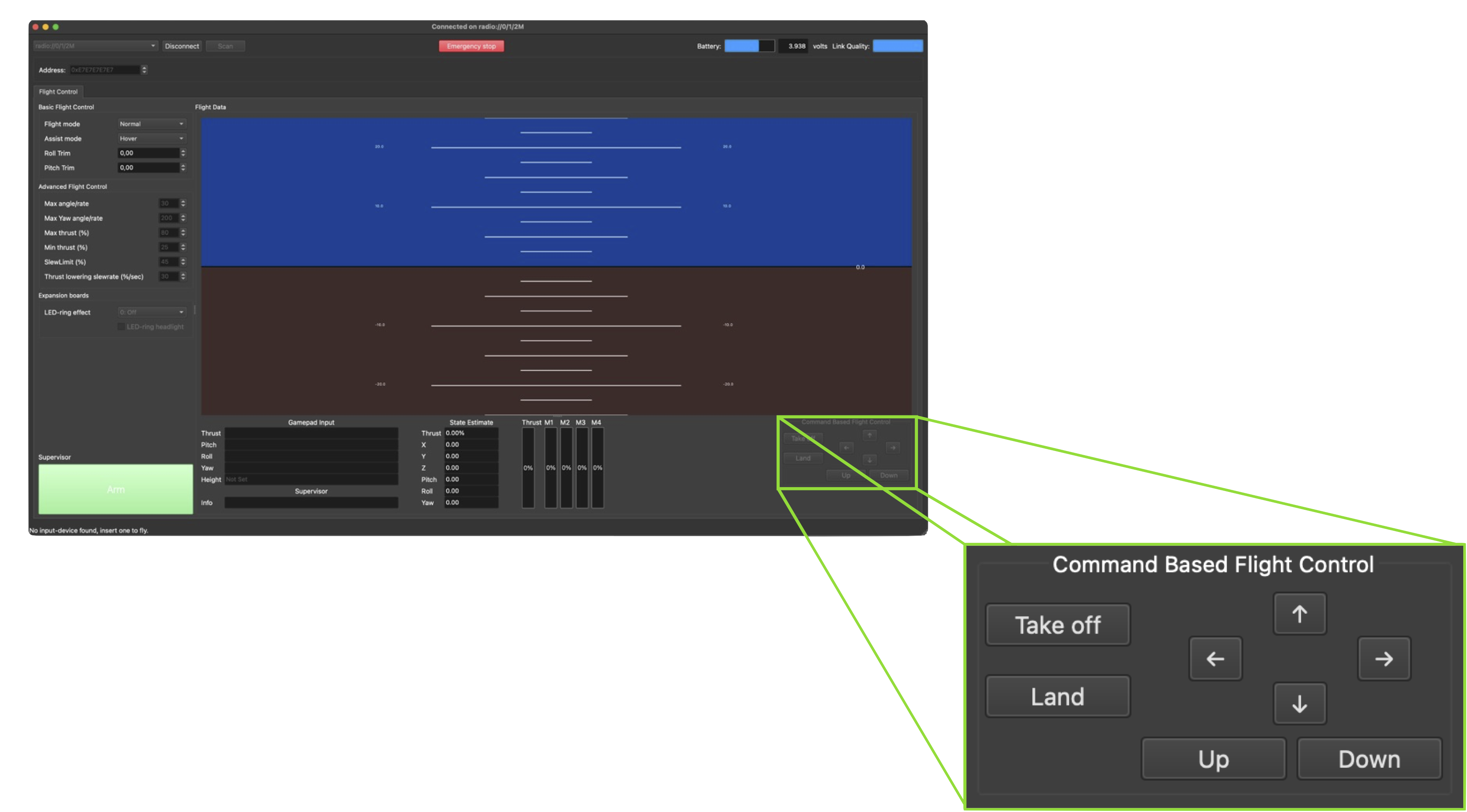
Conforme vimos anteriormente:

• Os botões Up e Down alteram a variável setpoint.position.z em incrementos de \(0,5\)
• Os botões ← e → alteram a variável setpoint.position.y em incrementos de \(0,5\)
• Os botões ↑ e ↓ alteram a variável setpoint.position.x em incrementos de \(0,5\)

Vamos continuar utilizando os botões Up / Down para comandar a força total \(f_t\) em incrementos de \(0,01\,N\), mas agora os botões ↑ / ↓ e ← / → vão comandar, respectivamente, os ângulos de Euler de referência \(\theta_r\) e \(\phi_r\) em incrementos de \(\frac{\pi}{4} \text{rad}\) (\(45^{\circ}\)). Para tal, precisamos ajustar as escalas da seguinte forma:

Abaixo temos um exemplo de função reference() que faz isso:

// Get reference setpoints from commander module
void reference()
{
    // Declare variables that store the most recent setpoint and state from commander
    static setpoint_t setpoint;
    static state_t state;

    // Retrieve the current commanded setpoints and state from commander module
    commanderGetSetpoint(&setpoint, &state);

    // Extract position references from the received setpoint
    ft =  (setpoint.position.z * 2.0f) / 100.0f;      // Thrust force command [N] (maps 0.5m -> 0.01N)
    phi_r = (setpoint.position.y * 2.0f) * pi/4.0f;   // Roll reference command [rad] (maps 0.5m -> pi/4 rad)
    theta_r = (setpoint.position.y * 2.0f) * pi/4.0f; // Pitch reference command [rad] (maps 0.5m -> pi/4 rad)
    psi_r = 0.0f;                                     // Yaw reference command [rad]
}

Controlador de atitude

A função attitudeController() é quem comanda os torques a partir da diferença entre os ângulos de Euler de referência e estimados.

// Compute desired torques
void attitudeController()
{ 
}

Para projetar um controlador, precisamos de um modelo da planta que será controlada. Já vimos que a dinâmica linearizada de um quadricóptero pode ser representada pelo diagrama de blocos abaixo:

Como a dinâmica de atitude de cada ângulo está desacoplada, é possível controlar cada um deles individualmente. Toda a técnica de controle explorada aqui será realizada para o ângulo de inclinação \(\theta\), e a mesma será replicada depois para os ângulos de rolagem \(\phi\) e guinagem \(\psi\).

A dinâmica de inclinação pode ser representada pelo diagrama de blocos abaixo:

Podemos cancelar o momento de inércia da planta de modo que a variável de controle seja a aceleração angular, conforme abaixo:

Isso reduz o sistema a ser controlado a um integrador duplo. Vamos detalhar três possíveis controladores para um sistema como esse, ficando a seu critério qual utilizar:

• Controlador proporcional derivativo (PD)
• Controlador proporcional em cascata (P-P)
• Regulador quadrático linear (LQR)

PDP-PLQR

O controlador proporcional derivativo (PD) combina ações proporcional e derivativa para reagir tanto ao erro quanto à sua variação, oferecendo boa resposta e bom amortecimento. É simples de implementar e eficaz para o integrador duplo, mas sua sensibilidade ao ruído na derivada pode limitar o desempenho.

Definição dos ganhos \(k_p\) e \(k_d\)

O diagrama de blocos acima pode ser representado por uma função de transferência do controlador \(C(s)\) e outra da planta \(G(s)\):

a) Escreva as funções de transferência do controlador \(C(s)\) e da planta $G(s)

\[ C(s) = I_{yy} \left( k_p + k_d s \right) \qquad \qquad G(s) = \dfrac{1}{I_{yy}s^2} \]

b) Determine a função de transferência em malha fechada \(T(s)\)

\[ \begin{align} T(s) &= \dfrac{G(s)C(s)}{1+G(s)C(s)} \\ T(s) &= \dfrac{\frac{1}{\cancel{I_{yy}}s^2} \cancel{I_{yy}} \left( k_p + k_d s \right)}{1+ \frac{1}{\cancel{I_{yy}}s^2} \cancel{I_{yy}} \left( k_p + k_d s \right)} \\ T(s) &= \dfrac{\frac{k_p + k_d s}{s^2}}{\frac{s^2}{s^2}+\frac{k_p + k_d s}{s^2}} \\ T(s) &= \dfrac{\frac{k_p + k_d s}{\cancel{s^2}}}{\frac{s^2 + k_p + k_d s}{\cancel{s^2}}} \\ T(s) &= \dfrac{k_d s + k_p}{s^2 + k_d s + k_p} \end{align} \]

c) Escreva os ganhos \(k_p\) e \(k_d\) em função da frequência natural \(\omega_n\) e do fator de amortecimento \(\zeta\) do sistema em malha fechada

\[ T(s) = k \frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + \omega_n^2} \quad \longrightarrow \quad \left\{ \begin{array}{l} k_p = \omega_n^2 \\ k_d = 2 \zeta \omega_n \end{array} \right. \]

d) Calcule os ganhos \(k_p\) e \(k_d\) para que a dinâmica de atitude do quadricóptero tenha um tempo de acomodação de \(0,3s\) e uma ultrapassagem percentual de \(0,5\%\)

\[ \begin{align} \zeta &= \dfrac{|\ln(OS)|}{\sqrt{\ln^2(OS)+\pi^2}} \\ \zeta &= \dfrac{|\ln(0,005)|}{\sqrt{\ln^2(0,005)+\pi^2}} \\ \zeta &= 0,86 \end{align} \]

\[ \begin{align} k_p &= \omega_n^2 \\ k_p &= 15,50^2 \\ k_p &= 240,28 \end{align} \]

\[ \begin{align} \omega_n &= \dfrac{4}{\zeta T_s} \\ \omega_n &= \dfrac{4}{0,86 \cdot 0,3} \\ \omega_n &= 15,50 \text{rad/s} \end{align} \]

\[ \begin{align} k_d &= 2 \zeta \omega_n \\ k_d &= 2 \cdot 0,86 \cdot 15,50 \\ k_d &= 26,67 \end{align} \]

O controlador proporcional derivativo insere um zero no sistema, assim um dos polos da origem vai até o zero e o outro até menos infinito, conforme o diagrama de lugar das raízes abaixo:

Olhando o controlador isoladamente, temos o seguinte diagrama de blocos:

Que se traduz nas equações abaixo:

\[ \left\{ \begin{array}{l} \theta_e = {\color{var(--c3)}\theta_r} -{\color{var(--c1)}\theta} \\ {\color{var(--c2)}\tau_y} = I_{yy} \left( k_p \theta_e + k_d \dfrac{d \theta_e}{dt} \right) \\ \end{array} \right. \]

Inclua na função attitudeController() duas variáveis locais \(k_p\) e \(k_d\), que correspondem aos ganhos do controlador, e, em seguida, calcule o torque comandado \({\color{var(--c2)}\tau_y}\)(1).

1. O termo derivativo \(z_d = \dfrac{d \theta_e}{dt}\) pode ser calculado com uma variável auxiliar conforme exemplo abaixo.

// Compute desired torques
void attitudeController()
{
    // Controller parameters (settling time of 0.3s and overshoot of 0,05%)
    static const float kp = 
    static const float kd = 

    // Compute angle error
    float theta_e = 

    // Calculate derivative term with auxiliary variable of previous error (static to retain value amoung function calls)
    static float theta_e_prev;
    theta_d = (theta_e-theta_e_prev)/dt;
    theta_e_prev = theta_e;

    // Compute desired torque
    ty = 
}

O controlador proporcional em cascata (P-P) utiliza duas malhas hierárquicas — uma interna e outra externa — o que melhora a estabilidade e o tempo de resposta. É intuitivo e robusto, mas requer ajuste cuidadoso entre as duas malhas para evitar oscilações.

Definição dos ganhos \(k_p\) e \(k_d\)

O diagrama de blocos acima pode ser representado por duas funções de transferência do controlador \(C_1(s)\) e \(C_2(s)\) e outras duas da planta \(G_1(s)\) e \(G_2(s)\):

a) Escreva as funções de transferência do controlador \(C_1(s)\) e \(C_2(s)\) e da planta \(G_1(s)\) e \(G_2(s)\)

\[ C_1(s) = I_{yy} k_d \qquad \qquad C_2(s) = k_p \qquad \qquad G_1(s) = \dfrac{1}{I_{yy}s} \qquad \qquad G_2(s) = \dfrac{1}{s} \]

b) Determine a função de transferência em malha fechada \(T_1(s)\)

\[ \begin{align} T_1(s) &= \dfrac{G_1(s)C_1(s)}{1+G_1(s)C_1(s)} \\ T_1(s) &= \dfrac{\frac{1}{\cancel{I_{yy}}s} \cancel{I_{yy}}k_d }{1+\frac{1}{\cancel{I_{yy}}s} \cancel{I_{yy}}k_d} \\ T_1(s) &= \dfrac{\frac{k_d}{s}}{\frac{s}{s}+\frac{k_d}{s}} \\ T_1(s) &= \dfrac{\frac{k_d}{\cancel{s}}}{\frac{s + k_d}{\cancel{s}}} \\ T_1(s) &= \dfrac{k_d}{s + k_d} \end{align} \]

c) Determine a função de transferência em malha fechada \(T_2(s)\)

\[ \begin{align} T_2(s) &= \dfrac{G_2(s)T_1(s)C_2(s)}{1+G_2(s)T_1(s)C_2(s)} \\ T_2(s) &= \dfrac{\frac{1}{s}\frac{k_d}{s + k_d}k_p}{1+\frac{1}{s}\frac{k_d}{s + k_d}k_p} \\ T_2(s) &= \dfrac{\frac{k_d k_p}{s^2 + k_ds}}{\frac{s^2 + k_ds}{s^2 + k_ds}+\frac{k_d k_p}{s^2 + k_ds}} \\ T_2(s) &= \dfrac{\frac{k_d k_p}{\cancel{s^2 + k_ds}}}{\frac{s^2 + k_ds + k_d k_p}{\cancel{s^2 + k_ds}}} \\ T_2(s) &= \dfrac{k_d k_p}{s^2 + k_d s + k_d k_p} \end{align} \]

d) Escreva os ganhos \(k_p\) e \(k_d\) em função da frequência natural \(\omega_n\) e do fator de amortecimento \(\zeta\) do sistema em malha fechada

\[ T(s) = k \frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + \omega_n^2} \quad \longrightarrow \quad \left\{ \begin{array}{l} k_p = \dfrac{\omega_n}{2\zeta} \\ k_d = 2 \zeta \omega_n \end{array} \right. \]

e) Calcule os ganhos \(k_p\) e \(k_d\) para que a dinâmica de atitude do quadricóptero tenha um tempo de acomodação de \(0,3s\) e uma ultrapassagem percentual de \(0,5\%\)

\[ \begin{align} \zeta &= \dfrac{|\ln(OS)|}{\sqrt{\ln^2(OS)+\pi^2}} \\ \zeta &= \dfrac{|\ln(0,005)|}{\sqrt{\ln^2(0,005)+\pi^2}} \\ \zeta &= 0,86 \end{align} \]

\[ \begin{align} k_p &= \frac{\omega_n}{2\zeta} \\ k_p &= \frac{15,50}{2\cdot0,86} \\ k_p &= 9,01 \end{align} \]

\[ \begin{align} \omega_n &= \dfrac{4}{\zeta T_s} \\ \omega_n &= \dfrac{4}{0,86 \cdot 0,3} \\ \omega_n &= 15,50 \text{rad/s} \end{align} \]

\[ \begin{align} k_d &= 2 \zeta \omega_n \\ k_d &= 2 \cdot 0,86 \cdot 15,50 \\ k_d &= 26,67 \end{align} \]

O ganho \(k_d\) determina a localização do polo da malha de controle interna:

Já o ganho \(k_p\) determina a localização dos polos da malha de controle externa:

Caso o ganho \(k_d\) seja suficientemente maior (\(>5\times\)) que o ganho \(k_p\) , o polo em \(-k_d\) é desprezível e a malha de controle externa se comporta como um sistema de 1ª ordem cuja constante de tempo é dada apenas pelo polo em \(-k_p\):

A ideia de um controlador em cascata é projetar malhas de controle sucessivamente mais lentas de modo que as malhas internas possam ser aproximadas a um ganho unitário constante. No entanto, é preciso tomar cuidado. Se o ganho da malha de controle interna for muito alto, isso pode gerar saturação dos atuadores.

f) Calcule os ganhos \(k_p\) e \(k_d\) para que o a dinâmica de atitude do quadricóptero tenha um tempo de acomodação de \(0,3s\) e que o polo mais rápido seja desprezível

\[ \begin{align} \tau &= \dfrac{T_s}{4} \\ \tau &= \dfrac{0,3}{4} \\ \tau &= 0,075 \end{align} \]

\[ \begin{align} k_p &= \dfrac{1}{\tau} \\ k_p &= \dfrac{1}{0,075} \\ k_p &= 13,33 \end{align} \]

\[ \begin{align} k_d &= 5 k_p \\ k_d &= 5 \cdot 13,33 \\ k_d &= 66,65 \end{align} \]

Olhando o controlador isoladamente, temos o seguinte diagrama de blocos:

Que se traduz na equação abaixo(1):

1. No sistema linearizado temos que \({\color{var(--c1)}\dot{\theta}} = {\color{var(--c1)}\omega_y}\)

\[ {\color{var(--c2)}\tau_y} = I_{yy} \left( k_d \left( k_p \left( {\color{var(--c3)}\theta_r} - {\color{var(--c1)}\theta} \right) - {\color{var(--c1)}\omega_y} \right) \right) \]

Inclua na função attitudeController() duas variáveis locais \(k_p\) e \(k_d\), que correspondem aos ganhos do controlador, e, em seguida, calcule o torque comandado \({\color{var(--c2)}\tau_y}\).

// Compute desired torques
void attitudeController()
{
    // Controller parameters (settling time of 0.3s and overshoot of 0,05%)
    static const float kp = 
    static const float kd = 

    // Compute desired torque
    ty = 
}

O regulador quadrático linear (LQR) realimenta todas as variáveis do sistema e permite posicionar os polos em locais desejados do plano complexo, atendendo diretamente aos requisitos dinâmicos de desempenho. É o mais simples e preciso dos três em termos de sintonia e resposta, mas exige domínio do formalismo de espaço de estados.

Definição dos ganhos \(k_p\) e \(k_d\)

A dinâmica de atitude pode ser representada pelo seguinte sistema de equações diferenciais:

\[ \left\{ \begin{array}{l} \begin{bmatrix} \dot{\theta} \\ \ddot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{I_{yy}} \end{bmatrix} \tau_{\theta} \\ \\ \theta = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} \end{array} \right. \]

Ou através da representação no espaço dos estados:

Onde:

\[ u = \tau_{\theta} \qquad x = \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix} \qquad y = \theta \qquad A = \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \qquad B = \begin{bmatrix} 0 \\ \frac{1}{I_{yy}} \end{bmatrix} \qquad C = \begin{bmatrix} 1 & 0 \end{bmatrix} \]

Um regulador de estados consiste em realimentar todos os estados do sistema simultaneamente ao invés de apenas a saída(1), conforme o diagrama de blocos abaixo:

1. Para fazer uma analogia entre controle por realimentação do estados (controle moderno) e controle por realimentação da saída (controle clássico), vamos considerar um médico tratando um doente com febre alta:

   • Se o médico tratar o doente segundo os conceitos de controle clássico, ele vai medir a temperatura do paciente e vai dar um remédio para abaixar a febre quando ela estiver alta e não fazer nada quando a febre estiver baixa.
   • Se o médico tratar o doente segundo os conceitos de controle moderno, ele vai examinar o paciente, identificar a causa da febre e dar um remédio para a doença e não para a febre (ou seja, o médico vai tratar a doença eliminando a causa da febre e não somente o sintoma da doença).

   O grande problema do controle por realimentação dos estados é exigir que os estados do sistema estejam disponíveis para serem realimentados, ou seja, é necessário medir todos os estados do sistema ou pelo menos estimá-los.

Onde:

\[ x_r = \begin{bmatrix} \theta_r \\ \dot{\theta}_r \end{bmatrix} \qquad K = I_{yy} \begin{bmatrix} k_p & k_d \end{bmatrix} \]

Como estamos aplicando um realimentação de estados do tipo:

\[ u = K \left( x_r - x \right) \]

A dinâmica em malha fechada fica:

\[ \begin{align} \dot{x} &= Ax + Bu \\ \dot{x} &= Ax + BK(x_r - x) \\ \dot{x} &= \underbrace{(A-BK)}_{A_{mf}}x + \underbrace{BK}_{B_{mf}}x_r \end{align} \]

a) Determine a matriz de transmissão dos estados em malha fechada \(A_{mf}\)

\[ \begin{align} A_{mf} &= A - BK \\ A_{mf} &= \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} - \begin{bmatrix} 0 \\ \frac{1}{\cancel{I_{yy}}} \end{bmatrix} \cancel{I_{yy}} \begin{bmatrix} k_p & k_d \end{bmatrix} \\ A_{mf} &= \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} - \begin{bmatrix} 0 & 0 \\ k_p & k_d \end{bmatrix} \\ A_{mf} &= \begin{bmatrix} 0 & 1 \\ -k_p & -k_d \end{bmatrix} \end{align} \]

b) Determine o polinômio característica do sistema em malha fechada \(p(s) = \det \left( sI - A_{mf} \right)\)

\[ \begin{align} p(s) &= \det \left( sI - A_{mf} \right) \\ p(s) &= \det \left( s \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} 0 & 1 \\ -k_p & -k_d \end{bmatrix} \right) \\ p(s) &= \det \begin{bmatrix} s & -1 \\ k_p & s+k_d \end{bmatrix} \\ p(s) &= s \left( s + K_k \right) - k_p \left( -1 \right) \\ p(s) &= s^2 + k_d s + k_p \end{align} \]

c) Escreva os ganhos \(k_p\) e \(k_d\) em função da frequência natural \(\omega_n\) e do fator de amortecimento \(\zeta\) do sistema em malha fechada

\[ p(s) = s^2 + 2 \zeta \omega_n s + \omega_n^2 \quad \longrightarrow \quad \left\{ \begin{array}{l} k_p = \omega_n^2 \\ k_d = 2 \zeta \omega_n \end{array} \right. \]

d) Calcule os ganhos \(k_p\) e \(k_d\) para que a dinâmica de atitude do quadricóptero tenha um tempo de acomodação de \(0,3s\) e uma ultrapassagem percentual de \(0,5\%\)

\[ \begin{align} \zeta &= \dfrac{|\ln(OS)|}{\sqrt{\ln^2(OS)+\pi^2}} \\ \zeta &= \dfrac{|\ln(0,005)|}{\sqrt{\ln^2(0,005)+\pi^2}} \\ \zeta &= 0,86 \end{align} \]

\[ \begin{align} k_p &= \omega_n^2 \\ k_p &= 15,50^2 \\ k_p &= 240,28 \end{align} \]

\[ \begin{align} \omega_n &= \dfrac{4}{\zeta T_s} \\ \omega_n &= \dfrac{4}{0,86 \cdot 0,3} \\ \omega_n &= 15,50 \text{rad/s} \end{align} \]

\[ \begin{align} k_d &= 2 \zeta \omega_n \\ k_d &= 2 \cdot 0,86 \cdot 15,50 \\ k_d &= 26,67 \end{align} \]

Olhando o controlador isoladamente, temos o seguinte diagrama de blocos:

Que se traduz na equação abaixo(1):

1. No sistema linearizado temos que \({\color{var(--c1)}\dot{\theta}} = {\color{var(--c1)}\omega_y}\). Além disso, como o objetivo é deixar o quadricóptero estacionário, a velocidade angular de referência \({\color{var(--c3)}\dot{\theta}_r}\) pode ser assumida como sendo zero, o que reduz o segundo termo:

   \[ k_d \left( \cancelto{0}{{\color{var(--c3)}\dot{\theta}_r}} - {\color{var(--c1)}\dot{\theta}} \right) = - k_d {\color{var(--c1)}\omega_y} \]

\[ {\color{var(--c2)}\tau_y} = I_{yy} \left( k_p \left( {\color{var(--c3)}\theta_r} - {\color{var(--c1)}\theta} \right) - k_d {\color{var(--c1)}\omega_y} \right) \]

Inclua na função attitudeController() duas variáveis locais \(k_p\) e \(k_d\), que correspondem aos ganhos do controlador, e, em seguida, calcule o torque comandado \({\color{var(--c2)}\tau_y}\).

// Compute desired torques
void attitudeController()
{
    // Controller parameters (settling time of 0.3s and overshoot of 0,05%)
    static const float kp = 
    static const float kd = 

    // Compute desired torque
    ty = 
}

Note que, ao invés de realimentar os ângulos e velocidades angulares reais, você está realimentando os ângulos e velocidades angulares estimados. Ou seja, você está supondo que o estimador de atitude desenvolvido anteriormente é perfeito. Isso é chamado de "observed-based control" e é um método muito típico para estruturar sistemas de controle.

---

Validação

Para validar o seu controlador você irá realizar dois experimentos. Em ambos os experimentos você deve colocar um pequeno valor de força de empuxo \(f_t\).

Controle de um grau de liberdade

O primeiro experimento consiste em controlar o drone em apenas um grau de liberdade. Você irá utilizar um dispositivo criado especificamente para isso, que restringe todos os graus de liberdade do drone deixando apenas o ângulo de inclinação \(\theta\) livre.

Para testar o controlador você pode aplicar distúrbios no quadricóptero (dando um "tapinha" na parta inferior de seus motores) e verificar se o mesmo retorna ao ângulo de referência \(\theta_r=0^{\circ}\). Você pode também alterar o ângulo de referência para, por exemplo, \(\theta_r=45^{\circ}\), através do Crazyflie Client, e ver se o quadricoptero se inclina sozinho.

Controle de três graus de liberdade

O outro experimento consiste em controlar o drone em três graus de liberdade. No entanto, como os módulos dos controladores vertical e horizontal ainda não foram implementados, você irá realizar isso através de uma queda livre controlada.

Altere a função attitudeController() de modo que ela comande não só o torque \(\tau_y\) como também os torques \(\tau_x\) e \(\tau_z\)(1).

1. Por conta da simetria do drone, você deve utilizar os mesmos ganhos \(k_p\) e \(k_d\) para o ângulo de rolagem \(\phi\) e inclinação \(\theta\). No entanto, para o ângulo de guinagem \(\psi\), recomenda-se utilizar um ganho \(k_p\) 4x menor e um ganho \(k_d\) 2x menor, que corresponde à mesma ultrapassagem percentual de \(0,5\%\) mas a um tempo de acomodação 2x maior (\(0,3s \rightarrow 0,6s\)).

// Compute desired torques
void attitudeController()
{
    // Controller parameters (settling time of 0.3s and overshoot of 0,05%)
    static const float kp = 
    static const float kd = 

    // Compute desired torques
    tx = 
    ty = 
    tz = 
}

Segure o quadricóptero a uma distância de aproximadamente \(50\text{cm}\) do chão e, assim que os motores começarem a girar, solte ele. Ele deverá cair devagar (comparado a uma queda livre) e sem rotacionar em torno de nenhum eixo.